つまらないことばかり考えていました。
その結実(経過)がこの程度です。
「和と積分」
和の極限が積分で
差の極限が微分か
「立方数の和」で書いた和の公式は
つまるところ積分に関係しているようです。
和の公式は整数の和、
積分は連続実数の和とも言えそうです。
1^3+2^3+・・+n^3=(1+2+・・+n)^2 ------------(1)
=(n(n+1)/2)^2 -------------(2)
(1)は、積分にも当てはまるようです。
積分の公式:
∫x^p dx = (1/(p+1))x^(p+1)
=x^(p+1)/(p+1) ------------------(3)
(情けない積分記号と x(エックス)で申し訳ないですが・・)
積分の範囲は(0からn)までの定積分として、
以下その表記を省略します。
∫ x^3 dx =(∫ x dx)^2 --------------------------(4)
=n^4/4=(n^2/2)^2=(n・n/2)^2 -----(5)
(4)と(1)は、ともに「3乗の和」が「和の2乗」になる -------(6)
ということを意味しているようです。
(2)と(5)は、その値としての式が少し似ています。 ---------(7)
(7)に関連して、
2乗の積分は、
∫x^2 dx = n^3/3 -------------------------------(8)
平方数の公式は、
1^2+2^2+・・+n^2=n(n+1)(2n+1)/6 -------(9)
(一見すると全然似てないようですが、少し変形すると)
=n(n+1)2(n+(1/2))/6
=n(n+(1/2))(n+1)/3 ----------------(10)
これは(8)の積分の (n・n・n)/3 に少し似ています。----(11)
少し近い、少し似ている和の公式と積分は、もちろん
等しくはなりません。
さらに、(2)と(5)、(10)と(11)を比べると分かるように
和の公式は積分より大きいようです。
図1 上昇曲線なので
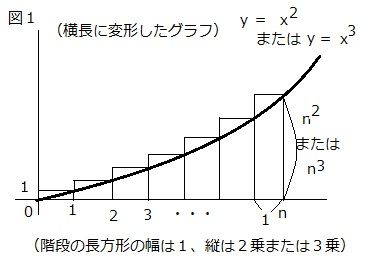
図に示したつもりのように、
積分は曲線下の面積ですが、和の公式は
曲線に沿って描いた長方形の集まり、つまり階段の面積だからです。
図によって、和の公式>積分 であることも分かると思います。
しかし図の長方形の幅を限りなく狭くして
長方形の数を限りなく増やすと曲線下の面積になります。
私が若い頃には、その極限値を求めて、
曲線下の面積を求めることから積分に入ったような記憶があります。
今は、微分の逆を積分として、そのうえで
積分が曲線下の面積であることを証明しているようでした。
そちらのほうが私も分かりやすくはあるのですが・・・
以上、お粗末でした。
昔書いたこと
過去は忘却の積分であり
現在は喪失の微分である
(2013年09月19日)

コメント